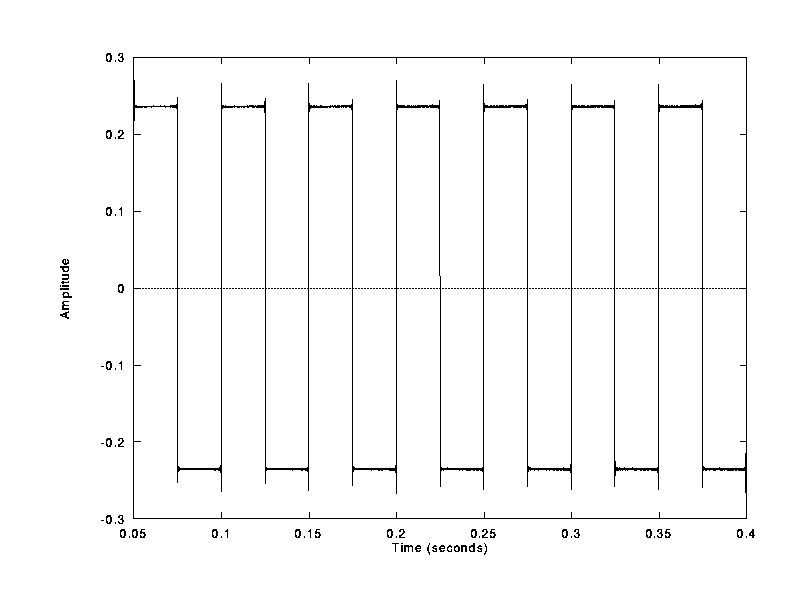Additive Synthesis on the T0 Vector Microprocessor
For my Master's project, I was working with the
T0 / Torrent project, led by Prof.
John Wawrzynek,
writing an additive synthesis core for the T0
vector microprocessor. Co-contributers include
Adrian Freed and
David Wessel
from the
Center for New Music and Audio Technology (CNMAT), and
John Hauser from CS.
The synthesizer is a software package
that performs additive synthesis of music. It is written
in a combination of C and assembly code to run on the SPERT
boards installed in Sun workstations at ICSI (and elsewhere in the
world). The additive technique produces sound by summing a group
of sine waves (partials) at differing frequencies, amplitudes, and
phases. This contrasts with techniques such as sampling, FM, physical
modelling, or subtractive. The set of sine waves -- the sound -- is
produced via this method because it is convieniently paired with
a process called analysis/resynthesis,. During analysis, a set of
sound sources are converted into a format --- called a spectral
description -- that exposes the frequency content of the sounds
and provides information about how they are spectrally related to one another.
Then, during resysnthesis, these spectral descriptions are manipulated
and combined in real-time by a performer to create fades, morphs, filtering, etc
with very fine control over timbre.
We use various software at CNMAT to provide analysis and
real-time manipulations (e.g., Adrian's "BYO"). The resulting input stream
is sent to the synthesis software, and the sound from the synth sent
to a D/A converter for output.
The key novel idea in our sythesizer was the recasting of the recursion
equation for the sine computation, keeping error outside the bounds of
auditory perception while minimizing the number of additional
operations required to implement the modified equation on our
hardware. Additionally, this technique is a good match to the
vector-style architectures -- SIMD, VLIW, multimedia (small-data-type
vector) ISA extensions like MMX -- that are becoming more common in
advanced processors.
A nice short (4-page) version of the work is the
ICASSP 1999
paper.
Sound Example
Here is a ten second tenor voice resynthesis with ten partials and
128 samples per frame. The first was generated using 32-bit IEEE
floating-point for the filter, while the second uses the modified
form for T0. Audibly the waveforms are indistinguishable,
but physically they differ.

Visual Example
A square wave with 500 partials spanning from 20 to
19980Hz at 44.1KHz sampling rate. Square waves are nice visual examples because
the error is easily estimated.
Technical Abstract
The most widely used digital sinusoidal oscillator structure employs a first order recursion to accumulate and
wrap a phasor, followed by a sinusoidal functional evaluation - usually a table lookup. Second order recursions
are an attractive alternative because the sinusoid is computed within the structure, avoiding the need for a large
table or specialized hardware function evaluator. Unfortunately, numerous theoretical and practical challenges
have to be overcome to use second order structures. We were motivated to overcome these because the next
generation of microprocessors are hostile to efficient implementations of first order oscillators. Although primary
cache memory may be large enough to hold a sine table, no locality of reference is observed for arbitrary
frequencies. Good performance from vector microprocessors such as the "T0", "TigerSharc", "Altivec" and VLIW
machines such as "Merced" requires exploitation of their strength - large multiply/add rate for on-chip data.
The primary challenge with digital recursive structures is managing long-term stability, since rounding and
truncation errors accumulate. In most applications frequency precision is the primary concern so the slow,
long-term phase drift of first order oscillators can be ignored. Error accumulation is much more serious in second
order structures and unfortunately the most efficient second order structure, the direct form I, is the most
susceptible to debilitating instability at musically useful frequencies. This was particularly evident in our first
implementations on T0, a microprocessor with a 16-bit fixed point vector arithmetic core. For this architecture we
periodically recompute the state variables of the second order recursion at sufficient precision thereby eliminating
error accumulation within the inner loop recursions. For these oscillators to be musically useful we also had to
address the frequency precision problem, especially troublesome for low frequencies. A novel coefficient coding
scheme and slightly more expensive filter structure solved this within perceptually significant bounds. An
overlap/add strategy for the filter outputs addressed the final challenge - smoothly interpolated frequencies and
amplitudes for banks of oscillators.
Technical Abstract (another version)
There are many benefits in the use of additive synthesis for
sound production in computer music applications. The challenge of the
technique is its voracious appetite for separately controllable
sinusoidal partials.
This paper summarizes our work developing a real-time additive
synthesis engine supporting hundreds of simultaneous partials
using the T0 vector microprocessor. The goal was to provide
significantly more real-time partials than were available using
conventional general-purpose hardware architectures.
The major features of T0 that drive the design is the vector ISA
and the use of fixed-point arithmetic. The explicit parallelism
of the vector ISA led us to use parallel recursive oscillators. The
16b fixed-point arithmetic required adapting the recursive oscillators
to provide additional accuracy.
The modified oscillator is a two-pole filter that maintains frequency
precision at a cost of one additional operation per filter sample.
The new filter's error properties are expressly imperfect, explicitly
matched to use in the context of digital audio (i.e., the human
auditory system) rather than general-purpose applications.
We briefly describe the controlling synthesizer software,
the control structure for feeding the oscillators, fast initialization
(needed for short additive synthesis windows), and
applicability to related architectures.
We present algorithm performance analysis and measurements of the
implementation, focusing on how chip features affected algorithm design
choices. The technique achieves 608 simultaneous real-time partials at
44.1KHz with the processor running at 40MHz and performing 8 operations
per cycle (peak), or about 1.5 cycles per partial per sample.

Todd Hodes,
<mylastname @ myfullname dot org>