First for a spherical distribution:

and second for a distribution of space-separated cubes:
Various geometries:
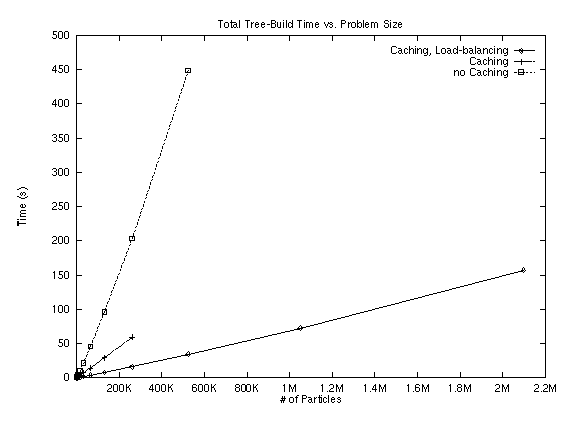
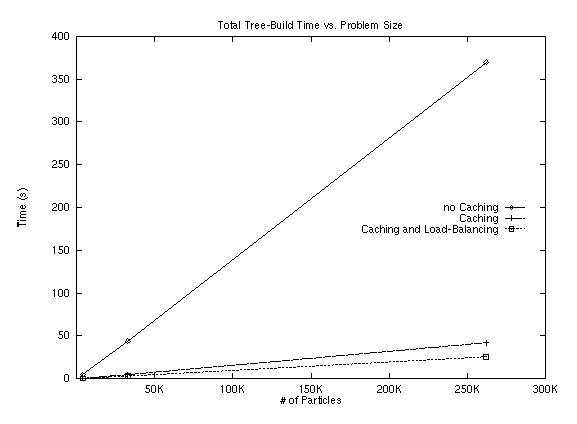
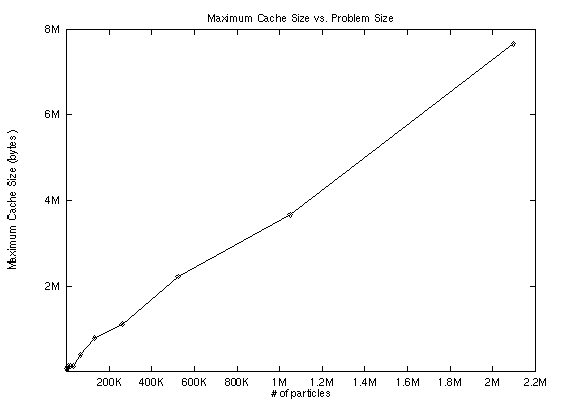
Lock contention in Parallel tree-build:
One piece of information not provided in the Splash-2 papers was the number of retries for acquiring the lock on a node. Our implementation has many fewer locks because we only lock to split a leaf. Regardless, in some runs with 4096 bodies, we saw in excess of 12,000 retries for a lock. This indicates that it is very important that the algorithm process multiple insertions at a single time. This benefits the program in two ways. First, handling multiple insertions at a single time will allow overlapping the addition of bodies into leaves, and retrieval of internal nodes if necessary. Second, it will reduce lock contention because a processor can work on inserting another body, which may end up being stored locally while it is waiting for the lock to become free.
Overhead from running the O(n log n) algorithm
The O(n^2) algorithm runs at about 40,000 interactions/node/sec. This is limited mainly by the speed of calculating the interaction, which involves 20-30 floating point operations (depending on how you count the work of a sqrt and divide). The O(n log n) algorithm prints out its results in terms of how many operations would be necessary with the O(n^2) algorithm. Doing this makes the O(n log n) algorithm look very good, it is running at about 500,000 interactions/second for a 16,384 body problem. However, taking the actual number of interactions that are calculated (both body-body and body-node), we found the algorithm is only performing about 2,000 interactions/second, all of the rest of the work is going into walking the tree and building the tree. Now, since we know that tree build for 16,384 nodes takes about 1 second, and that each step takes about 20 seconds, we find that tree-build only accounts for 5% of the work, and hence the majority of the work is being done in walking the tree. Therefore, if you are interested in running a relatively small simulation through very many time-steps, it is likely that the O(n^2) algorithm will run faster. Furthermore, it will have much fewer problems with errors. Warren and Salmon state in [10] (and show in great detail in [13]) that the error for the standard Barnes-Hut algorithm is unbounded. We show in the section on error bounds why this occurs in an explanation of how the tree walk and interaction works.
See pictures of evolving galaxies. Continue to Conclusions
-----
maintained by <hodes@cs.berkeley.edu>